3章:一般化線形モデル(GLM)-ポアソン回帰-/データ解析のための統計モデリング入門(緑本)のメモ
データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学) を読んでいる最中なのですが、実際に手を動かすのが大事ということなので備忘録として残します。
一般化線形モデル(GLM)とは
正規分布以外の確率分布を扱いたいときに使う線形モデル。
(一般)線形モデルの特徴は以下の2つ。
- 応答変数 y が正規分布に従う
- 応答変数 y の平均がパラメータの一次結合で表される
これを一般化させたものが一般化線形モデル。
- 応答変数 y が正規分布、二項分布、Poisson 分布など(厳密には「指数型分布族」に含まれる分布)に従う
- y の平均(や確率)をある関数で変化させたら、パラメータの一次結合で表わされる
参考
- 一般化線形モデル入門の入門
- MCMC と階層ベイズモデル
使うデータ
著者のWebサイトに置かれている、架空の植物100個体の種子数データを用います。 http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/poisson/data3a.csv
x:個体の体サイズ
y:種子数
f:施肥処理の値
使うライブラリ
今回はPythonでやります。
Rだとglm()でGLMのあてはめができるのに対し、Pythonだとstatsmodelsというライブラリが使えるとのこと。scikit-learnでもできるみたいです。
その他はお決まりのpandas(データ操作用)、numpy(行列演算用)、matplotlib(グラフ描画用)を使います。
import statsmodels.api as sm
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
データの取得
pandasのread_csv()メソッドを使います。
data = pd.read_csv("http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/poisson/data3a.csv")
データの概要
data.head()
y x f
0 6 8.31 C
1 6 9.44 C
2 6 9.50 C
3 12 9.07 C
4 10 10.16 C
pandasのdescribe()メソッドでデータの概要を確認します。
data.describe()
y x
count 100.000000 100.000000
mean 7.830000 10.089100
std 2.624881 1.008049
min 2.000000 7.190000
25% 6.000000 9.427500
50% 8.000000 10.155000
75% 10.000000 10.685000
max 15.000000 12.400000
データの可視化
統計モデリングにあたり、扱うデータを様々な図にして視覚的に把握しておくことが大事。
その際、データ同士の演算結果を図にするのはしばしば間違いのもとになるので、できるだけデータをそのまま用うのがよいとのこと。
fig1 = plt.figure()
ax1 = fig1.add_subplot(111)
ax1.scatter(data.x[data.f=="C"], data.y[data.f=="C"], label="C",)
ax1.scatter(data.x[data.f=="T"], data.y[data.f=="T"], label="T")
ax1.legend(loc='upper left')
plt.show(fig1)
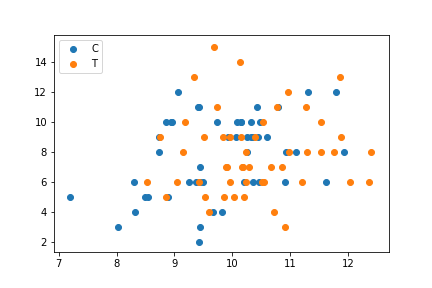
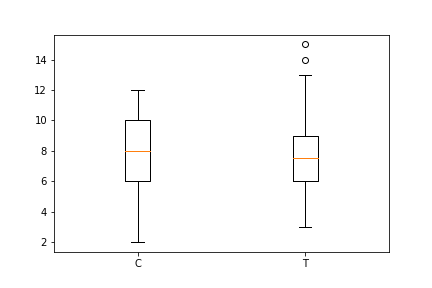
fig2 = plt.figure()
ax2 = fig2.add_subplot(111)
ax2.boxplot([data.y[data.f=="C"], data.y[data.f=="T"]], labels=["C", "T"])
plt.show(fig2)
ポアソン回帰による統計モデリング
ポアソン分布をつかてデータのばらつきを表現できそう。 個体ごとの平均種子数 λ が体サイズ x や施肥処理 f に影響を受けるモデルとなる。
個体 i において種子数が y である確率 p(y|λ) はポアソン分布にしたがうとして、
p(y|λ) = λ^y exp(-λ) / y!
と仮定する。ある個体 i の平均種子数 λ を、
λ = exp(β1 + β2 x)
と仮定し、両辺の対数をとると、
log λ = β1 + β2 x
左辺はリンク関数、右辺は線形予測子と呼ばれる。ポアソン回帰のGLMで対数リンク関数を使う理由は以下。
- 推定計算に都合がよい “ポアソン分布の平均は非負”という条件が、説明変数・パラメータの値によらず守られる
- わかりやすい 要因の効果が積で表される
対数尤度 log L が最大になるパラメータ β1 と β2 の推定値を決めることをポアソン回帰という。
このあてはめ(fitting)が手軽にできるライブラリがRでは用意されている。
Rの場合
model <- glm(y ~ x, data = d, family = poisson)
今回は Python の statsmodels というライブラリを使ってみます。
x = sm.add_constant(np.array(data.x).reshape(-1, 1))
y = np.array(data.y).reshape(-1, 1)
model1 = sm.GLM(y, x, family=sm.families.Poisson())
res1 = model1.fit()
res1.summary()
Generalized Linear Model Regression Results
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -235.39
Date: Sun, 01 Oct 2017 Deviance: 84.993
Time: 22:07:28 Pearson chi2: 83.8
No. Iterations: 4
coef std err z P>|z| [0.025 0.975]
const 1.2917 0.364 3.552 0.000 0.579 2.005
x1 0.0757 0.036 2.125 0.034 0.006 0.145
constは切片、x1は傾きに対応しています。
coef:推定値
std err:標準偏差
z:z値(Wald統計量)
Pr(>|z|):この場合に限定して言えば,平均が z 値の絶対値であり,標準偏差が1の正規分布におけるマイナス無限大からゼロまでの値をとる確率
これらより以下が導かれます。
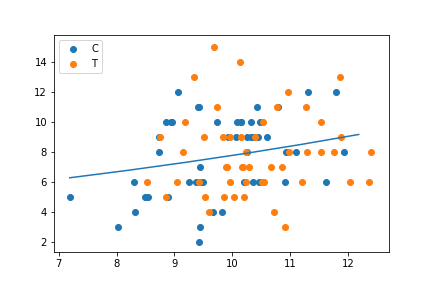
λ = exp(1.29 + 0.0757 x)
これを可視化します。
xx = np.arange(min(data.x), max(data.x), 1)
fig1 = plt.figure()
ax1 = fig1.add_subplot(111)
ax1.scatter(data.x[data.f=="C"], data.y[data.f=="C"], label="C",)
ax1.scatter(data.x[data.f=="T"], data.y[data.f=="T"], label="T")
ax1.plot(xx, np.exp(1.2917+0.0757*xx))
ax1.legend(loc='upper left')
plt.show(fig1)
fig1.savefig('glm.png')
因子型の施肥効果fを説明変数に組み込んでも同様にモデリングできます。
今回は以上です。
これらを実行するにあたってjupyter notebookを使ったのですが、学習用にもってこいですね。
ただ、数式書きづらいな〜、そのままMarkdownで記述できないかな〜とか思っていたところ、ちょうどそのような内容で大変参考になる記事を見つけたので、次回は取り入れてみようと思います。
Jupyter (iPython) Notebookを使って技術ノート環境を構築する方法
おわり。まだつづく。

